Menentukan deret ke-n suatu deret polinomial (deret dengan beda bertingkat) dengan bilangan Pascal (oleh Rifki Ridha)

*note : butuh waktu berhari - hari bagi saya untuk menemukan metode ini, Saya harap Saya yang pertama menggunakan metode ini dan semoga dikembangkan algoritma penyelesaiannya di waktu kedepannya, aamiin.

Deret polinomial adalah deret yang dapat didefinisikan sebagai deret dengan fungsi dengan pangkat variabel terbesar lebih dari satu dan variabelnya sendiri adalah suku ke-n itu sendiri (Un = f(n)), atau juga bisa didefinisikan sebagai deret dengan beda bertingkat dengan tingkat lebih dari satu hingga tingkat ke bilangan tertentu bedanya adalah konstan. Jika beda pertama adalah konstan maka deret tersebut adalah deret linear/ deret aritmatika, dengan b=Un-U(n-1)

Beda tingkat ke-n adalah beda jika deret tersebut dikurangi akan menghasilkan beda pertama (tingkat pertama), jika tidak konstan maka beda tersebut diasumsikan deret lagi dan jika dihitung bedanya maka itu didefinisikan sebagai beda kedua (tingkat ke-2), beda tingkat ke-n belum tentu nilainya selalu sama..

Deret polinomial pangkat n adalah deret polinomial dengan beda tingkat ke-n adalah konstan.

misal :

1, 3, 5, 7, 9,... adalah deret linear

sebab beda antara suku ke-n dan suku sebelumnya (n-1) selalu sama yaitu 2

1, 4, 9, 16, 25.. adalah deret polinomial pangkat 2 -> beda tingkat 2
sebab f(n) = n^2 dengan n adalah suku ke n

Beda tingkat pertamanya tidak konstan,yaitu

(4-1),(9-4),(16-9),(25-16),... = 3, 5, 7, 9,...

Beda tingkat keduanya adalah
(5-3), (7-5), (9-7), ... = 2, 2, 2,.... (konstan)

1^k, 2^k, 3^k, 4^k,.... adalah deret bilangan pangkat k, dengan beda tingkat ke-k adalah konstan dengan nilai k! (k faktorial) (hasil analisis saya sendiri)

Deret Pascal dapat ditentukan dengan segitiga Pascal
Segitiga Pascal adalah suatu aturan geometri pada koefisien binomial dalam sebuah segitiga. 

segitiga Pascal :

1 > baris ke-0

1 1 > baris ke-1

1 2 1 > baris ke-2

13 3 1 > baris ke-3

1 4 6 4 1 > baris ke-4

....

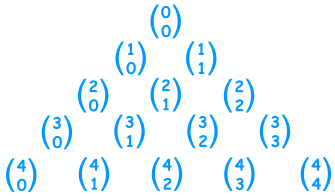
dalam bentuk kombinasi :

Suku ke-n deret polinomial dengan pangkat k atau beda tingkat ke-k nya adalah konstan dapat diselesaikan dengan menjumlahkan suku pertama deret tersebut dengan setiap beda tingkat ke-i yang pertama deret tersebut dikalikan dengan deret pascal ke-(i+1) baris ke (n-1)

sehingga didapatkan..

Contoh :

Menentukan suku ke-7 dan ke-8 dari deret 1, 16, 81, 256, 625, 1296...

Deret tersebut adalah deret fungsi pangkat 4, dengan beda ke 4 adalah 4! = 4 x 3 x 2 x 1 = 24

atau dapat ditelusuri dengan mencari bedanya, hasilnya terdapat pada tabel berikut

Sebenarnya ini adalah deret dengan suku ke n adalah f(n)=n^4

Namun jawaban tersebut dapat ditelusuri dengan rumus yang telah Saya tentukan dengan 

a=1, k=4, dan n=6 untuk suku ke-7 dan n=7 untuk suku ke-8

Hasil dari metode tesebut dapat dilihat pada tabel berikut :

Dapat dibuktikan dengan kalkulator U7=7^4 = 2401 dan U8=8^4=4096

Sehingga metode ini terbukti valid

Metode ini dapat digunakan untuk deret apa saja dengan syarat pada beda tingkat ke-k nya adalah konstan, dan metode ini tidak bisa digunakan untuk deret geometri karena tidak akan ditemukan beda-nya yang bernilai konstan.

Contoh deret geometri :
2, 4, 8, 16, 32...

 Metode ini dikembangkan oleh Rifki Ridha, metode ini adalah metode paling cepat jika Anda tidak bisa menentukan pola deret tersebut, Anda cukup mencari bedanya secara terus menerus hingga konstan dan Anda juga bisa merumuskan persamaan sendiri dengan menguraikan rumus kombinasinya dengan nCr = (n!)/((n-r)!*r!), jadi cara ini cukup efisien dan diharapkan program untuk metode ini dapat digunakan pada web jika ada yang ingin mengembangkan karena Saya sendiri belum menemukan metode ini di web dan belum menemukan juga aplikasi untuk menentukan deret ke-n sehingga metode ini adalah milik Saya jika belum ada yang mengembangkan, insha Allah Saya akan membuatkan programnya sehingga perhitungan bisa menjadi lebih efisien.

Metode lain yang tersedia (terdapat di buku matematika dan internet) adalah dengan cara mengeliminasi koefisien pada pola yang terdapat di deret, jika deret adalah pangkat n, maka bedanya memiliki n tingkat dan minimal harus memiliki suku sebanyak n untuk mengeliminasi koefisien pada persamaan tersebut sehingga didapatkan persamaan untuk deret ke-n.